Low-Rank Pruning of Llama2

Table of Contents

Introduction

Model pruning refers to the process of removing redundant information from machine learning models to make them “leaner”. As a result, the pruned model is smaller in size and should run faster which is suitable for deployment on resource-constrained devices or in real-time applications. Pruning can be combined with other techniques such as quantization to further optimize runtime. The most popular pruning approaches are based on discarding neurons, layer channels or entire layers. This kind of pruning is referred to as “sparsification”.

In practice however, sparse pruning has many limitations. In order to achieve actual speed-up in practice, custom sparsity-aware matrix multiplication (matmul) operations are required. For the moment, this is only partially supported in Ampere GPUs or on CPUs via NeuralMagic . In Pytorch, sparse matrix multiplication operations are not optimized. For example, there is no implementation available of the batched matmul operation with sparse matrices. Rewriting it with the existing operation requires some reshaping and the result is 2-3x slower performance.

Structured sparsity on the other hand consists in discarding weights in a structured way. For instance, we can remove columns, remove channels, block matrices, etc. This way, in theory, the model can be pruned without requiring specialized software/hardware for optimized runtime. Some structured sparsity methods still require optimized software to achieve faster runtime. For example, block-sparsity requires implementing dedicated GPU kernels for block-sparse matmul such as OpenAI's Block-sparse GPU kernels.

In practice however, structured sparsity cannot be pushed too far without a larger drop in accuracy compared to unstructured sparsity. As a result, the performance gain is usually very limited.

Low Rank Pruning

The idea of low-rank pruning revolves around factorizing the weight matrix W of a linear layer as a matrix multiplication of a pair of two matrices A and B, such that A and B have much less columns and rows respectively: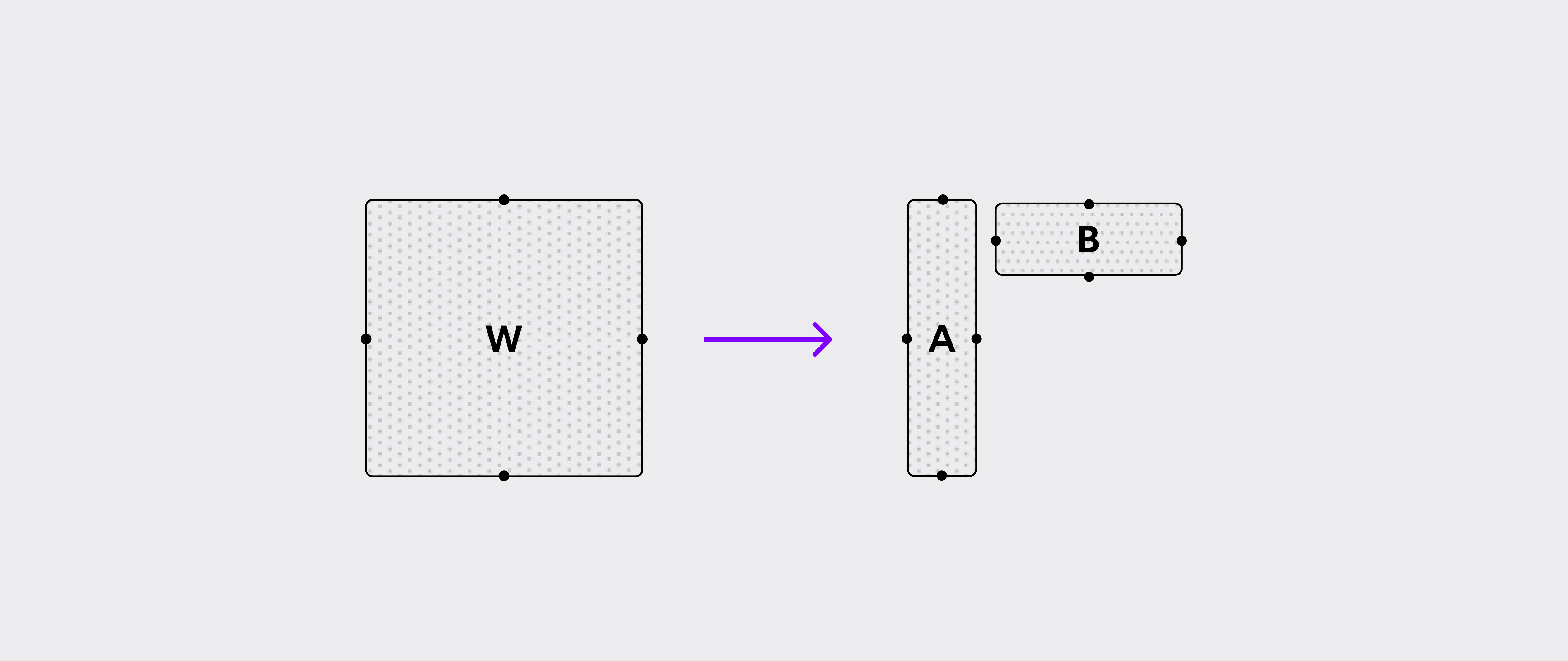

Ideally, we would like the chain matmul operation with A and B to be faster and take less memory, while the overall model prediction stays as close as possible to the original prediction with unaltered weights. We refer to the number of columns of A/number of rows of B as the maximum rank (denoted by max_rank) in the rest of the article.

There are various ways to achieve such a factorization (SVD, QR, etc.). We use the SVD decomposition as follows to get the matrix pairs:

The idea of using low-rankness is not new in the context of Transformer models. The adoption of low-rank estimation has garnered considerable attention, primarily within the domain of model compression. The works in https://arxiv.org/pdf/2004.04124.pdf and https://neurips2022-enlsp.github.io/papers/paper_33.pdf study low-rank compression of BERT and GPT models, respectively. An additional approach, documented in https://openreview.net/pdf?id=uPv9Y3gmAI5, employs weighted low-rank estimation to compress BERT-based models. Furthermore, the research outlined in https://cs.nju.edu.cn/wujx/paper/AAAI2023_AFM.pdf explores an innovative perspective by focusing on low-rank compression of the model features, as opposed to the model weights.

Among these approaches, one that has gained significant popularity is LoRA (Low-Rank Adaptation). LoRA's core concept revolves around training supplementary low-rank parameters to adapt large models. This technique enables the training of expansive models while drastically reducing the memory requirements.

Pruning typically requires fine-tuning on a large dataset, which is very expensive even for smaller LLM models such as LLama2-7B. We find that, by applying low-rank estimation, freezing the weights and leveraging LoRA instead for custom training, we can achieve significant efficiency as we explain in the next section.

Low-Rank Pruning of Llama2 Models

When we analyze the weights of the Llama2-7B model, we find that many are in fact already low-rank, especially those of the attention layers (Q,K,O). The graph below shows the distribution of the average normalized singular values per layer type. We normalize the singular values by the highest value (which is the same as normalizing the matrix weight by its L2 norm) so we can average the singular values across the layers and get a single plot per layer type. We can clearly see that most of the energy is concentrated in a subset of the singular values. More specifically, about 80% of the energy is concentrated in the first half of the singular values of the Q,K,V,O layers of the attention modules. The first layers of the attention module tend to have an even lower-rank. For instance, 88% of the energy of the first Q layer is concentrated in the first 1024 (25%) of its singular values.

In practice, we found that the rank of the original attention and MLP layers can be reduced from 4096 to 1024 and 2048 respectively, while still delivering good performance after LoRA training. This is a 4x rank reduction in the attention layers and 2x for the MLP layers, which is quite aggressive given that these weights are frozen after pruning.

We summarize the steps for training and inference using the proposed approach:

Training Mode

• For each linear layer, we run SVD on the weights of the linear layers W to get the A,B matrix pairs such that the matrix multiplication AB estimates W using the predefined max_rank value to truncate the singular values as explained in the previous section. The only layer that we keep full-rank is the v_proj. This is because the rank of the weights of this layer tends to be higher.
• We freeze all the weights and use LoRA with the r parameter to create the new trainable parameters.

Inference mode

After training, we need to re-estimate new pairs of matrices that combine the original low-rank weights and the newly trained LoRA weights:

• For each linear layer that was pruned, we have the A,B as well as the LoRA pairs that we refer to as AL,BL
• Since the rank of the sum of two matrices is lower or equal than the sum of their ranks $$ {rank({\bf AB}+{\bf A_L} {\bf B_L} ) \le rank({\bf AB}) + rank({\bf A_LB_L})} $$ we can safely combine the 4 weights by applying truncated SVD on the sum of their matrix multiplications using the sum of their ranks to build the new low-rank pair: $$ {\bf AB} + {\bf A_LB_L} \Longrightarrow{\bf \bar{A}\bar{B}}$$ $$ { rank({\bf \bar{A}\bar{B}} ) = \text{max_rank} + \text{r} } $$
• Now we can use the new pair and remove the older A,B and LoRA weights.

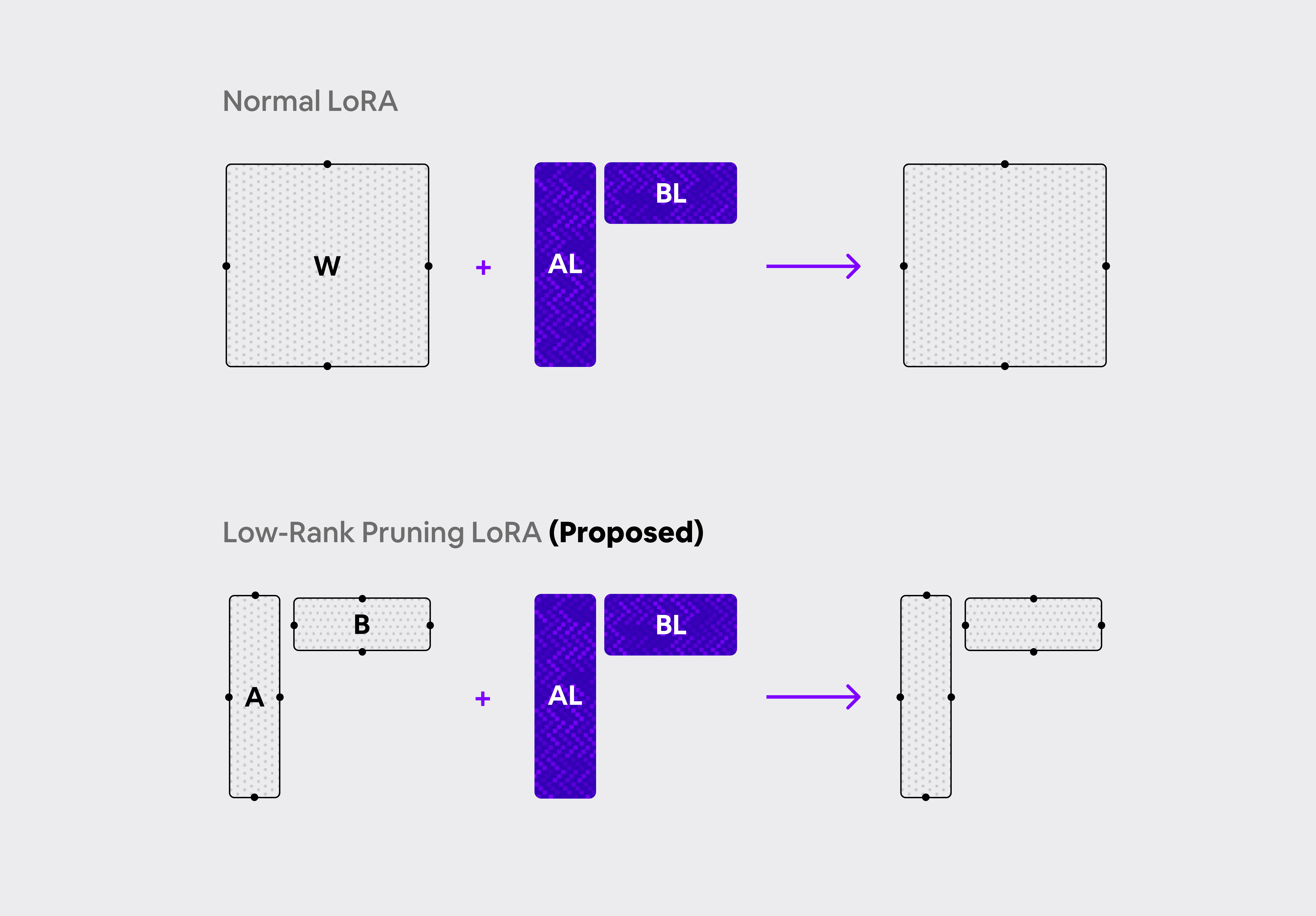
The illustration below shows the difference between the standard LoRA approach and the proposed low-rank LoRA merging method. Note that the result is a pair of matrices.

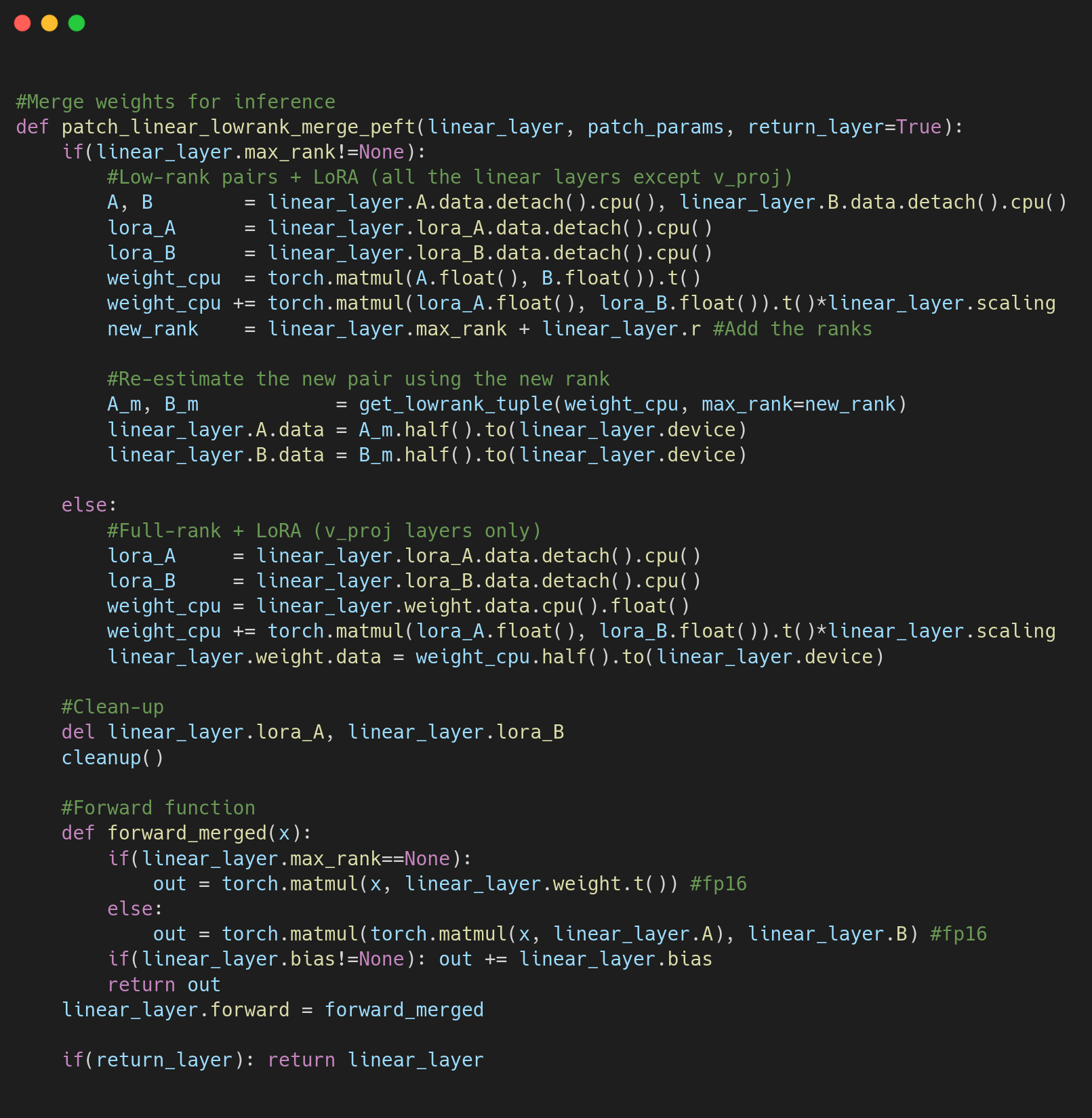
The code below summarizes the merging logic:

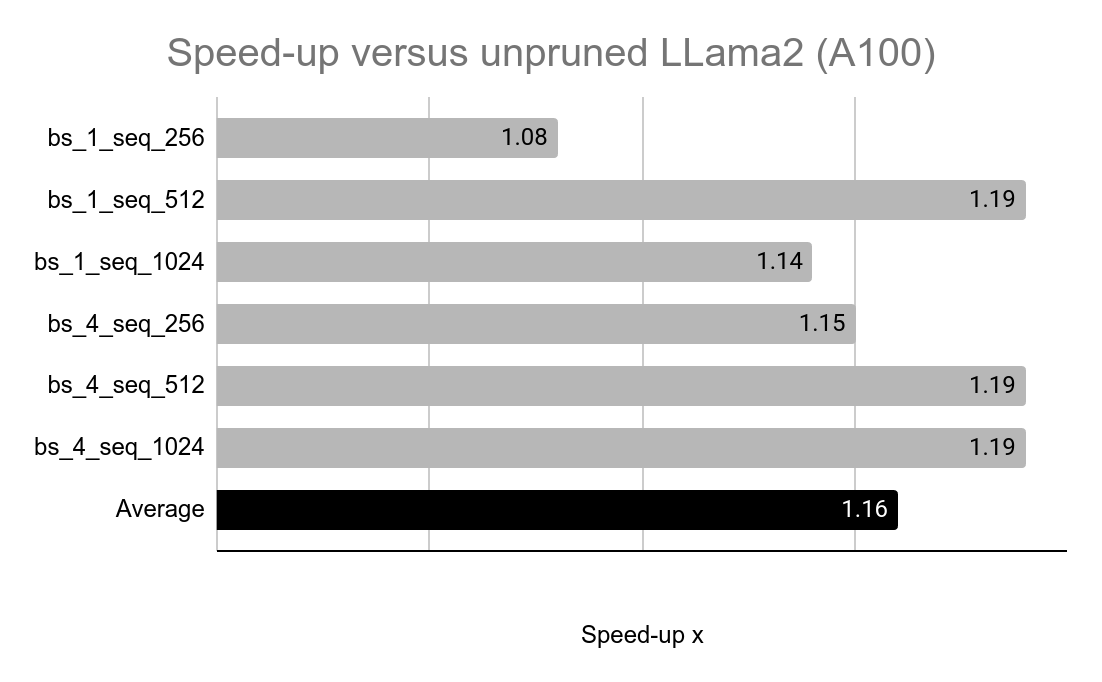
Speed Benchmark

We report the inference speed-up in comparison to the original LLama2-7B model. We employ the HuggingFace implementations with fp16 precision. When we merge the LoRA weights into the original model, the resulting matrices maintain the same dimensions as those in the original model. However, in the pruned version, the rank of the matrices increases by the LoRA rank r. For instance, in the attention layers, the initial weight matrix W has dimensions of 4096x4096. By using a rank of 2048 and a LoRA rank of 32, the resulting pairs A and B will be 4096x2080 and 2080x4096, respectively. Reducing the rank leads to a faster speed boost but has a detrimental effect on prediction accuracy.

Dataset Performance

We present performance results on 5 datasets, evaluating both the unaltered and pruned LLama2-7B models using the perplexity metric. In the case of the original model, we use the default LoRA settings (r=8). Conversely, in the pruned model, we raise the LoRA rank to 32. Remarkably, the pruned model exhibits strong performance despite the removal of approximately half of the original weights, all without any fine-tuning!

It is worth noting that the performance of the pruned model on OpenOrca-1M is better than that of the original model on 100k samples. This indicates that the pruned model has the capacity to learn but needs more samples to compensate for the noise introduced by pruning.

Dataset	LLama2-7B	LLama2-7B pruned
vicgalle/alpaca-gpt4	3.49	4.11
databricks/databricks-dolly-15k	4.13	5.86
knkarthick/dialogsum	3.78	4.82
ArtifactAI/arxiv-math-instruct-50k	3.08	3.73
Open-Orca/OpenOrca - 100k	3.51	4.27
Open-Orca/OpenOrca - 1M	-	3.43
Average	3.60	4.56

Conclusion

In this article, we've demonstrated the utility of low-rank pruning as an effective method for accelerating large language models like LLama2-7B. Unlike sparse pruning, which often requires custom hardware or software configurations to realize significant speed gains, low-rank pruning doesn't require specialized kernel operations and can seamlessly integrate with existing matrix multiplication (matmul) implementations.

Nevertheless, there is ample scope for further refinements, and we aspire for this article to serve as an inspiration to the research community. We encourage researchers to embrace low-rank pruning and explore its synergistic potential when combined with other pruning and quantization techniques.

We provide code examples at https://github.com/mobiusml/low-rank-llama2/tree/main/code

---