Gemlite: Towards Building Custom Low-Bit Fused CUDA Kernels
Current AI models are super-sized with great power and skill. However, with great power comes great computational demand. As these models grow larger, the need for compression techniques like quantization becomes crucial to ensure they run efficiently on available accelerated hardware such as GPUs.
Writing CUDA code from scratch to implement quantization-aware runtime can be a daunting task, especially for those new to GPU programming.
In this blog post, we aim to simplify this process. We present Gemlite, a collection of simple CUDA kernels designed to help developers easily create their own low-bit "fused" General Matrix-Vector Multiplication (GEMV) CUDA code. The goal of Gemlite is not to provide the fastest solution but to offer flexible, easy-to-understand, and customizable code, making it more accessible for beginners. Although some features are still missing, we believe that releasing this code to the community now can be highly beneficial, addressing the current lack of available low-bit kernels.
This blog post assumes a basic understanding of CUDA and model quantization. Before diving into the content, we recommend readers familiarize themselves with these concepts. The lectures from CUDA MODE provide excellent coverage of both topics.
Introduction
Large machine learning models, such as Large Language Models (LLMs), require quantization to reduce the resources needed to run them on accelerated hardware like GPUs. Techniques such as GPTQ, AWQ and HQQ are crucial for efficiently running LLMs, as it significantly lowers deployment costs and accelerates the inference runtime.
To actually achieve significant speed improvements with quantized models, a custom CUDA implementation is necessary. This involves creating a "fused" kernel that combines the dequantization step with the dot product calculation. The improvement in speed isn't due to a reduction in computation-in fact, the dequantization step adds more operations—but from more efficient memory access. Quantized weights allow us to access more elements with less memory reads. For example, eight 4-bit elements can be stored in a single 32-bit element, referred to as "bitpacking".
While excellent open-source solutions exist for 4-bit linear quantization, such as Marlin and tinygemm, quantization isn't limited to just 4-bit. Large models, especially Mixture-of-Experts, can operate effectively at lower bits like 3-bit and 2-bit without significantly impacting accuracy. Additionally, linear quantization is just one approach; other methods, such as LUT-based quantization, are also viable. Combining techniques like sparsity with quantization remains largely unexplored. Implementing fused CUDA kernels from scratch is quite difficult, and even with existing code, adapting it requires time and advanced CUDA expertise.
To address this accessibility challenge, we developed Gemlite, a collection of easy-to-customize CUDA kernels. Our goal with Gemlite isn't to provide the fastest low-bit kernels but to offer a user-friendly code base. This allows anyone with minimal CUDA knowledge to modify the code and implement their desired quantization method.
In the following sections, we explain how Gemlite works and how to use the code base to write a new custom kernel.
Gemlite
Overview
We follow a similar approach to some fast GEMV implementations available like Bruce-Lee-LY's implementation and FastGEMV. The main idea revolves around processing chunks of the input vector x within a group of threads/warp.
In our case, each warp can process 1 column across 32 threads, and each block can process 32 columns. There are 3 main steps:
- We cache the input vector in the shared memory first, since more than 1 column is processed per block.
- Each thread within a warp calculates a partial dot product after dequantizing a chunk on-the-fly.
- Warp-level reduction to sum the results from the warp.
Fig 1. CUDA Threads Overview.
The illustraction above shows how the different CUDA threads are organized. The blue box represents a block, which contains 32 warps. Each warp consists of a set of 32 threads. We want each thread to process a small chunk of the input, such that 1 warp (32 threads) processes one whole weight column. Once the threads finish processing the chunks, the results are aggregated via a warp-level reduction .
Shared Memory Caching
The initial step involves copying the input vector or batch activations into shared memory. All the threads within the same block can access the same shared memory. Since one block can process more than one weight column (32 in our case), caching the input in the shared memory is beneficial. Each thread handles a small portion of this copy operation, and we must ensure that the entire copy process is completed before proceeding to the dot product step via thread synchronization.
//Shared memory
extern __shared__ half x_shared[];
#pragma unroll
for (size_t i = 0; i < x_chunk_size; ++i) {
size_t x_idx = i * threads_per_block + threadIdx.x;
x_shared[x_idx] = x[x_idx];
}
__syncthreads();
In this example, we use fp16 activations. For 8-bit activations, one simply needs to change the dtype from half to int8_t. For dynamic quantization, we would also need to adjust this step, though the indexing logic relative to the threads will remain unchanged.
Fused Dot Product
Once the input is cached in the shared memory, each thread can begin calculating a partial dot product. This step involves understanding how the quantized weights are stored through bitpacking and how dequantization can be executed by configuring a few additional parameters.
Bitpacking
Let's revisit how linear dequantization works. Given floating-point weights W, linear quantization approximates these weights using the formula W = (W_uint - w_zero) / w_scale. Here, W_uint represents the quantized integer weights, w_zero is the zero-point, and w_scale is the scaling factor. Techniques like GPTQ, AWQ, and HQQ aim to estimate these three parameters as accurately as possible. Since sub-byte data types, such as 4-bit, are not natively supported, we need an alternative method to store the quantized weights efficiently.
Bitpacking is the process of storing multiple sub-byte elements within native data types like uint8 or int32. This process usually involves reshaping, performing bitwise operations, and occasionally applying zero-padding.
To design a versatile kernel that supports various quantization bitwidths, we use a universal 32-bit bitpacking approach. For odd bitwidths, padding the weights is required to ensure their size is a multiple of the bitwidth. Nonetheless, the packing algorithm itself remains consistent.
One crucial aspect of bitpacking is how the elements are tiled during the packing process. To ensure coalesced memory access, it is essential to bitpack elements with an offset that aligns with the number of threads per group (tile_size=32 in our case, as there are 32 threads in a warp). Without this adjustment, the kernel performance can degrade significantly due to sub-optimal memory access within the warp. This can be achieved by first reshaping the quantized tensor to fit the tile_size and then looping through to pack the elements as follows:
## Bitpacking (skipping the padding step for odd nbits)
step = 32 // nbits;
W_shape = W_q.shape
W_q = W_q.to(torch.int32).view(-1, tile_size)
i, shift = 0, 32 - nbits
W_q_packed = (W_q[i::step, :] << shift)
#Pack
for i in range(1, step):
shift -= nbits
W_q_packed |= (W_q[i::step, :] << shift)
#Final reshape (axis=1 format)
W_q_packed = W_q_packed.reshape(W_shape[0], W_shape[1] // step)
Dequantization
To support arbitrary bitwidths within the same CUDA kernel, we need to define the following parameters for each bitwidth:
elements_per_sample: the number of elements packed per 32-bit packed element.unpack_mask: the mask used for unpacking, typicallynbits^2 - 1.q_shifts: a list of bit-shifting values used to unpack the elements based on their position in the packed 32-bit value.loc_shifts: the index of the element to be processed by the thread within a warp. This array is not necessary for caching since it is independent of the quantization approach but is included to simplify the main loop for the user.
Let's consider 4-bit quantization as an example. Each 32-bit packed value contains 8 elements, so both loc_shifts and q_shifts would have 8 elements. The masking value unpack_mask to mask the shifted unpacked value would be 4^2 - 1 = 0xF. loc_shifts consists of serial multiples of the number of threads per group (32 in the case of a full warp). q_shifts contains the bit-shifting values needed to recover the unpacked values. For instance, the first element needs to be shifted by 32-4=28 bits and then masked by unpack_mask, the second element by 28-4=24 bits, and so on.
Below is the code to define these parameters. For other bitwidths, such as 2-bit, the user would only need to adjust these values accordingly; the fused kernel logic remains the same.
const size_t W_nbits = 4;
const unsigned int unpack_mask = 0xf; // W_nbits **2 - 1
const size_t elements_per_sample = 8; //packing_nbits=32 / W_nbits
const size_t loc_shifts[elements_per_sample] = {0 , threads_per_group , threads_per_group*2, threads_per_group*3,
threads_per_group*4, threads_per_group*5, threads_per_group*6, threads_per_group*7};
const uint8_t q_shifts[elements_per_sample] = {28, 24, 20, 16, 12, 8, 4, 0}; //32 - W_nbits*i
Once these parameters are defined, the fused dequantization/dot product operation simplifies to a loop that is independent of the bitwidth:
#pragma unroll
for (size_t j=0; j < elements_per_sample; j++){
float _x = static_cast<float>(x_shared[x_idx + loc_shifts[j]]); //read from shared memory
float _w = ((static_cast<float>(W_q >> q_shifts[j]) & unpack_mask) - w_zero) / w_scale; //dequantize
sum += _x * _w;
}
Accumulation
The user also needs to specify how the partial sums are accumulated within the kernel. Our tests on Ampere and Ada GPUs have shown no performance improvement when using half-precision versus float32 accumulation, even with vectorized intrinsics like __hfma2. Moreover, we observed that half-precision accumulation can introduce noticeable errors in dot products, depending on the input distribution.
For integer dot products (8-bit activations), one can use 32-bit accumulation directly with integer intrinsics such as __dp4a.
We offer various examples (fp16, fp32, int32 accumulation) that users can choose from, depending on their desired quantization algorithm logic.
Warp-level Reduction
Once the threads have calculated partial dot products, these partial sums need to be combined into the final result. This is accomplished via warp-level reduction. This is a standard step that does not depend on the quantization logic.
The primary consideration here is the accumulation dtype. Various dtypes are supported by the templated warpReduceSum<dtype> function defined in the utils header. In terms of performance, we have not observed significant differences in speed when using float instead of half-precision for warp-level accumulation. Users can adapt this step based on the chosen accumulation dtype.
//fp32 warp reduction -> convert to fp16 output
sum = warpReduceSum<float>(sum, threads_per_group);
if (group_lane_id == 0) {y[group_col] = __float2half(sum);}
Performance
We compare the performance of low-bit GEMV kernels built on top of Gemlite with other popular kernels such as Tinygemm and BitBlas. For 8-bit operations, we compare against TorchAO's 8-bit torch.compiled matmul, as presented in the gpt-fast blogpost. We report the average relative speed-up versus fp16 across various matrix shapes ranging from 4096x4096 to 24576x24576 with a batch size of 1. Results for the RTX 3090 and RTX 4090 GPUs are shown below:
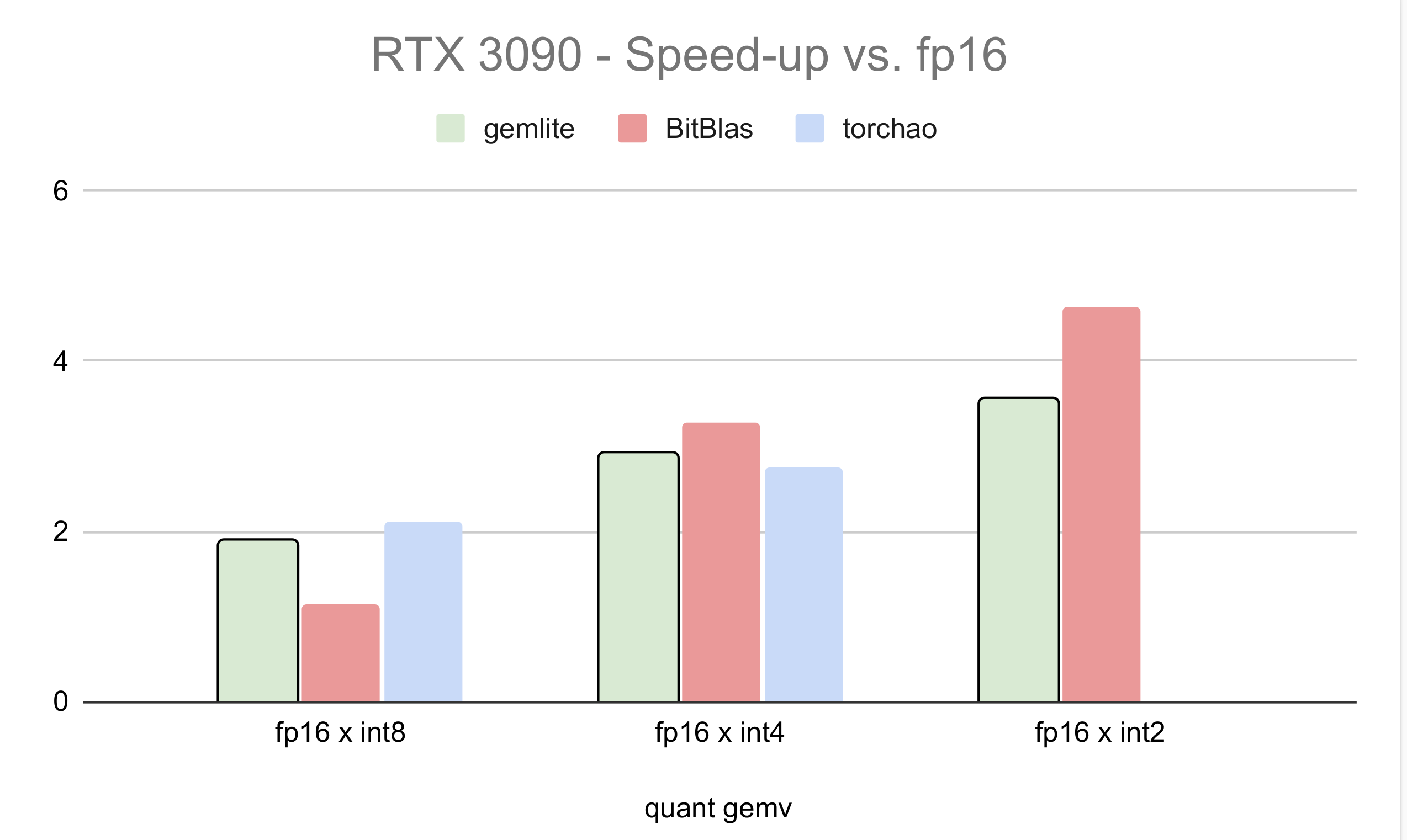
Fig 2. Relative Speed-Up Versus Half-Precision on the RTX 3090.
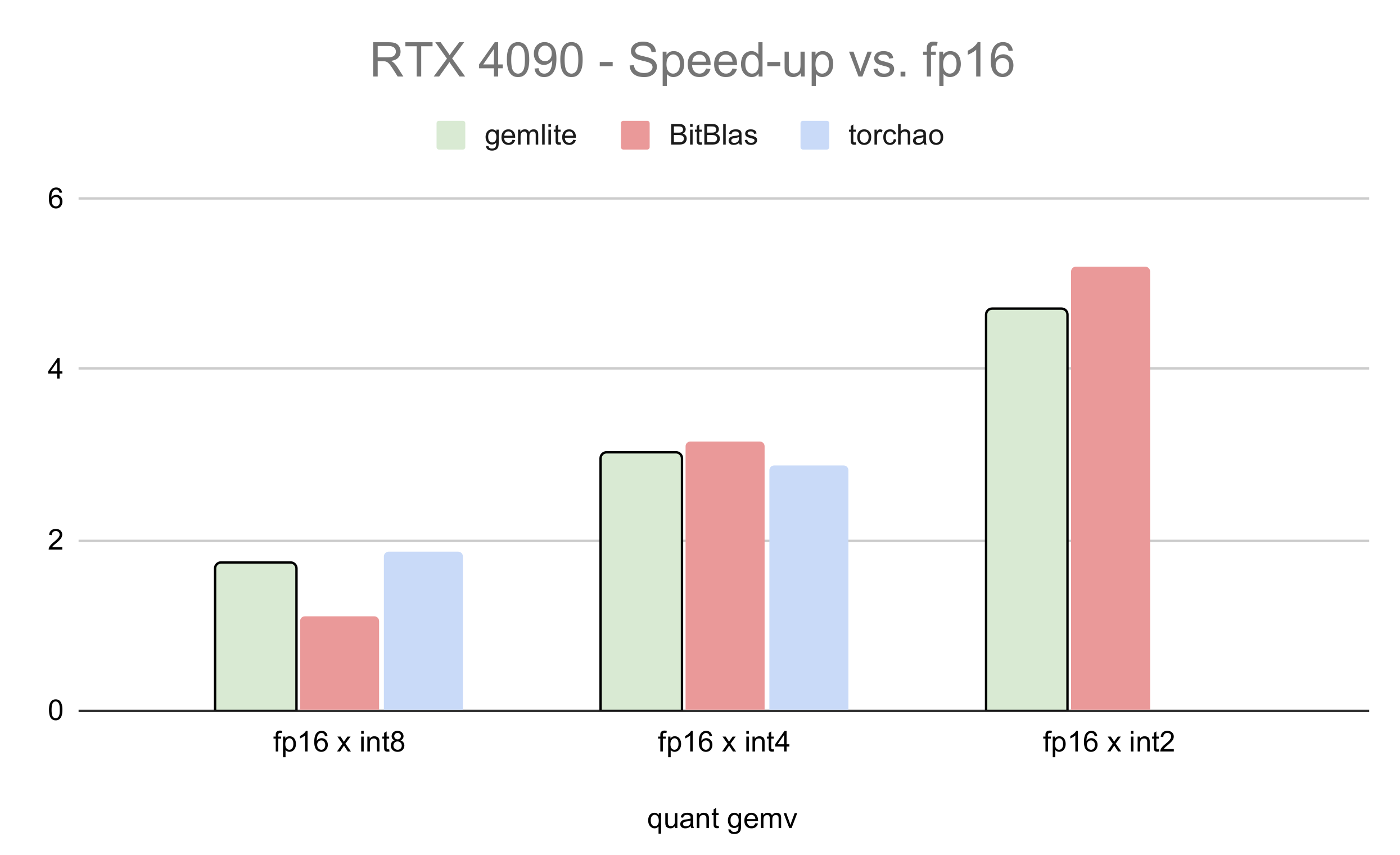
Fig 3. Relative Speed-Up Versus Half-Precision on the RTX 4090.
As shown, the Gemlite kernels perform competitively against the fastest available kernels for fused GEMV, despite being designed for user flexibility and easy adaptation to various bitwidths. We anticipate that specialized kernels built on top of Gemlite will achieve even higher performance, as the flexibility of the base Gemlite kernels can impact performance due to additional memory accesses and register usage.
Case Study: Mixed Quantization and 1:2 Sparsity
In this section, we demonstrate how to use the Gemlite codebase to build a custom fused kernel that combines quantization and sparsity, achieving up to 3.5x faster performance than Pytorch's fp16 matmul.
Approach
Semi-structured sparsity at a 50% level is known to result in minimal accuracy loss. In fact, 2:4 sparsity layouts are supported by modern GPUs by storing the non-zero values and using an additional 2-bit table that stores the sparsity information. This approach has been successfully used to accelerate architectures such as ViT.
However, combining semi-structured sparsity and quantization requires a more custom approach. Essentially, we want to leverage sparsity to compress the weights and reduce memory access through a custom bitpacking method. With semi-structured 1:2 sparsity, 1 out of 2 elements is non-zero and structured in a predefined way. By quantizing the non-zero element to 7 bits and using 1 bit to store the non-zero index, we can achieve a 4x compression rate similar to 4-bit quantization. The key difference is that the non-zero element is stored at a higher precision, resulting in minimal quantization degradation.
Implementation
Since the input and output are floating-point here, we use the kernel gemv_A16fWniO16f_fp32accfloat_int32pack_core_kernel defined in gemv_A16fWnO16f_int32packing.cu as a starting point. The only modification needed in the entire kernel is in the dequantization step, as we need to identify which of the packed elements is the non-zero.
First, let's explore how to bitpack the combined 1:2 sparse/7-bit quantized weight matrix. Similar to the default bitpacking logic explained in the previous section, we need to pack the 1:2 sparse elements in an interleaved manner. We can start by reshaping the matrix so that the columns match the number of threads per group (32 for a warp), then select the element with the highest magnitude for each pair of successive rows. This approach allows us to create a mask to sparsify the weight matrix, which can also be used during the backpropagation step to learn weights that are compatible with this sparsification approach. In this case, we supposed that the weights are already 7-bit quantized, with values ranging from 0 to 127.
def tiled_sparsity_50(W, tile_size=32):
#50% semi-structured sparsity with interleaved tiles
W_shape = W.shape
W_tiled_abs = W.view((-1, tile_size)).abs()
mask_chunk = W_tiled_abs[0::2,:] > W_tiled_abs[1::2,:]
mask = torch.zeros_like(W_tiled_abs)
mask[0::2, :] = mask_chunk
mask[1::2, :] = ~mask_chunk
return mask.reshape(W_shape)
This illustration demonstrates the structure of a reshaped weight matrix in pairs. The dark gray elements represent the 7-bit non-zeros, while the white elements indicate zeros. Notice the formation of pairs, where exactly one element is non-zero, and the other is zero.
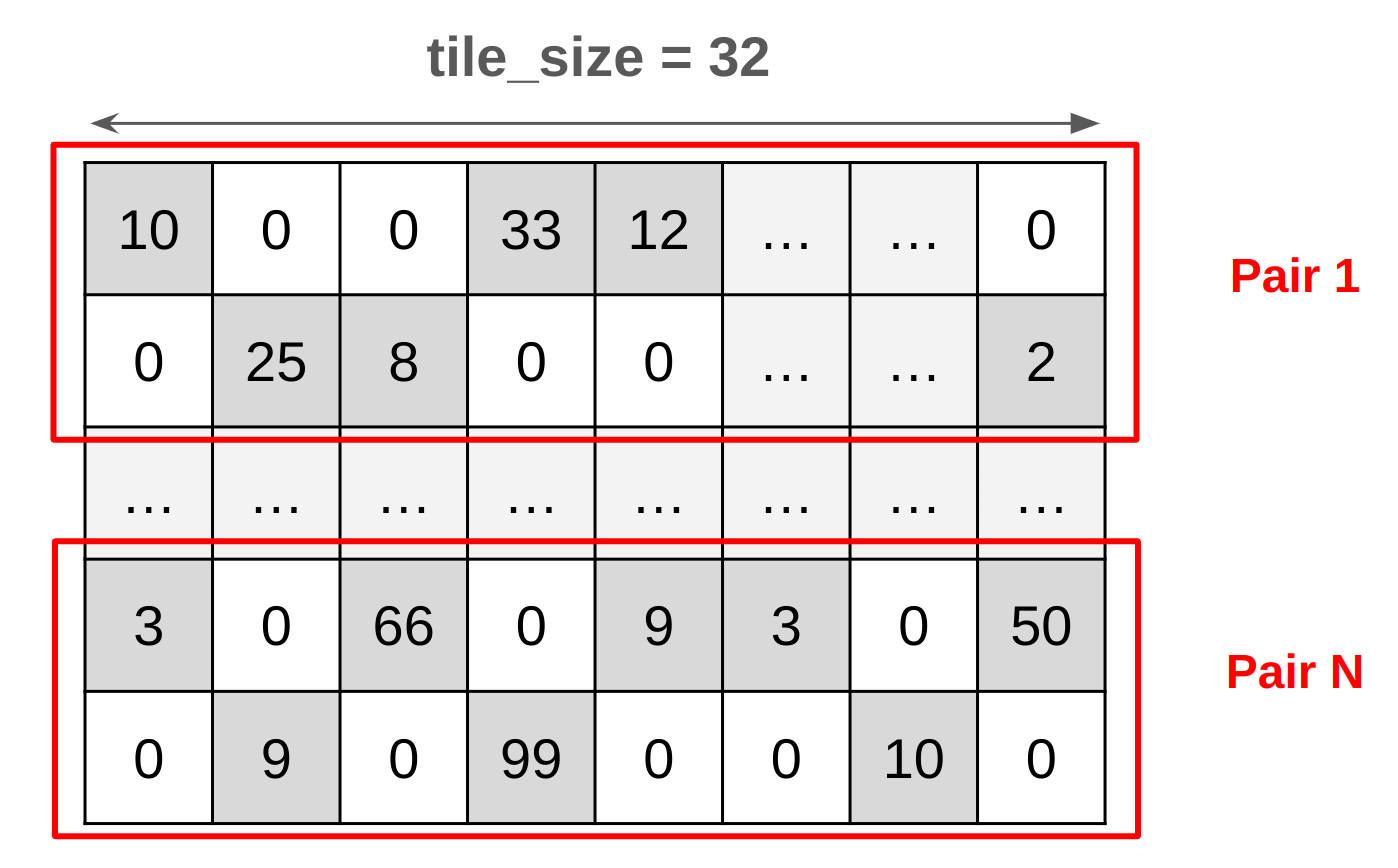
Fig 4. 1:2 Sparse/7-bit Weight Matrix Before Bitpacking.
We perform bitpacking as follows:
Obtain the sparsity mask as explained previously.
In each 8-bit integer, use the first 7 bits to store the non-zero value and the remaining bit to store its position (first=1, second=0).
Repeat this process four times to store 4 sparse/7-bit elements pairs in a single 32-bit packed value.
def pack_warped_int32_8bit_50_sparse(W_q, tile_size):
nbits = 8
step = 32 // nbits
sp_per_8bit = 2
W_shape = W_q.shape
W_q = W_q.to(torch.int32)
W_q = W_q.reshape(-1, tile_size)
#Mask
W_tiled_abs = W_q.abs()
mask_chunk = W_tiled_abs[0::2,:] > W_tiled_abs[1::2,:]
W_q_chunk1 = W_q[0::2,:] #pos0
W_q_chunk2 = W_q[1::2,:] #pos1
#Pack 2 7-bit/sparse chunks in 1-8bit
W_q_pos = mask_chunk.to(torch.uint8) #First 1-bit
W_q_val = W_q_chunk1 | W_q_chunk2 #2-8bit
W_q_8bit_ps = (W_q_val) | (W_q_pos<< 7)
# pos = (o >> 7) & 0b01111111
# val = (o >> 0) & 0b01111111
W_q_8bit_ps = W_q_8bit_ps.to(torch.int32)
W_q_packed = (W_q_8bit_ps[0::step, :] << 24)
W_q_packed |= (W_q_8bit_ps[1::step, :] << 16)
W_q_packed |= (W_q_8bit_ps[2::step, :] << 8)
W_q_packed |= (W_q_8bit_ps[3::step, :])
W_q_packed = W_q_packed.reshape(W_shape[0], W_shape[1] // (step*sp_per_8bit))
return W_q_packed
The illustration below shows how the pairs are stored using 8-bit representation. In this example, we have the following pairs (127, 0). 127, being the non-zero element, is located in the first position, which gives it an index of 1 that we put in the first bit in white. If the non-zero element were positioned second, it would be indexed with a 0 in the first bit instead. The remaining 7-bits represent the 127 non-zero value.

Fig 5. 1:2 sparse/7-bit Pair 8-bit Bitpacking Example.
On the CUDA side, we need to implement the dequantization step, which only requires changing the main body of the dot product loop, since the indexing logic remains unchanged. There are various ways to implement this step, but the approach is consistent: we recover the 8-bit elements from the 32-bit packed value. From each 8-bit element, we extract the 7-bit non-zero value (equivalent to a regular dequantization step), then use the remaining 1-bit to select which of the two elements is non-zero. The zero-element is skipped in the calculation, resulting in 50% fewer multiplications/additions compared to regular 4-bit quantization.
const uint8_t unpack_mask = 0xFF; //mask for unpacking the 8-bit pair
const uint8_t sp_unpack_mask = 0x7F; //mask to recover the non-zero element position in the pair
#pragma unroll
for (size_t i = 0; i < warp_iters; i += elements_per_sample) {
//... here goes the indices
//2x - chunk1
_w_q = (W_q >> 24) & unpack_mask;
_w = (static_cast<float>(_w_q & sp_unpack_mask) - w_zero) / w_scale;
_x = ((_w_q >> 7) & sp_unpack_mask) == 1 ? static_cast<float>(x_shared[x_idx + loc_shifts[0]]): static_cast<float>(x_shared[x_idx + loc_shifts[1]]);
sum += _x * _w;
//2x - chunk2
_w_q = (W_q >> 16) & unpack_mask;
_w = (static_cast<float>(_w_q & sp_unpack_mask) - w_zero) / w_scale;
_x = ((_w_q >> 7) & sp_unpack_mask) == 1 ? static_cast<float>(x_shared[x_idx + loc_shifts[2]]): static_cast<float>(x_shared[x_idx + loc_shifts[3]]);
sum += _x * _w;
//2x - chunk3
_w_q = (W_q >> 8) & unpack_mask;
_w = (static_cast<float>(_w_q & sp_unpack_mask) - w_zero) / w_scale;
_x = ((_w_q >> 7) & sp_unpack_mask) == 1 ? static_cast<float>(x_shared[x_idx + loc_shifts[4]]): static_cast<float>(x_shared[x_idx + loc_shifts[5]]);
sum += _x * _w;
//2x - chunk4
_w_q = (W_q >> 0) & unpack_mask;
_w = (static_cast<float>(_w_q & sp_unpack_mask) - w_zero) / w_scale;
_x = ((_w_q >> 7) & sp_unpack_mask) == 1 ? static_cast<float>(x_shared[x_idx + loc_shifts[6]]): static_cast<float>(x_shared[x_idx + loc_shifts[7]]);
sum += _x * _w;
}
The resulting kernel achieves up to a 3.5x speed-up compared to the fp16 version. The step to select the non-zero element here is not optimal, but for simplicity in this blog post, we use the ternary operator to make it easier for the reader to understand this step.
Conclusion
In this blog post, we presented Gemlite, a collection of simple CUDA kernels designed to facilitate the creation of custom low-bit GEMV kernels. We demonstrated how to use Gemlite to easily build a custom fast kernel that combines 1:2 sparsity with quantization. We hope the community finds this resource useful and that it inspires the development of innovative low-bit kernels.
Citation
@misc{badri2024gemlite,
title = {Gemlite: Towards Building Custom Low-Bit Fused CUDA Kernels,
url = {https://mobiusml.github.io/gemlite_blog/},
author = {Hicham Badri, Appu Shaji},
month = {August},
year = {2024}
}
Please feel free to contact us..
